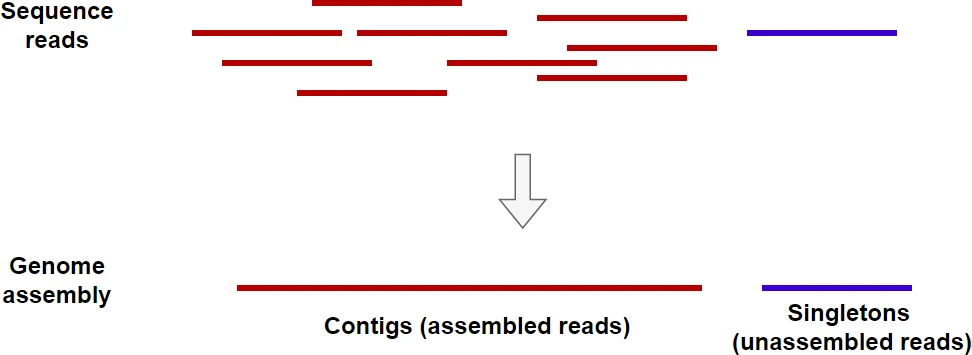
You can use samtools to calculate coverage depth and percent coverage from a BAM file.
samtools depth allows calculation of the coverage depth (how many times the given position is covered by the mapped read ) from the BAM file, whereas
samtools coverage allows calculation of how much percentages of bases are sequenced from the entire genome and chromosome..
The following examples explain how to use samtools depth and samtools coverage to calculate the coverage from a BAM file.
Before we begin, ensure that samtools is installed on your system. If not, you can read this article on installing samtools.
Samtools depth
samtools depth command can be used for calculating the coverage depth at each position (per-base coverage) or region of the reference genome.
samtools depth is similar to samtools mpileup with some changes in parameters, output, and offers speed benefit.
Calculate the coverage depth at each position,
samtools depth input.bam > coverage.txt
# view coverage.txt
head coverage.txt
chr1 10145 1
chr1 10146 1
chr1 10147 1
chr1 10148 2
chr1 10149 3
samtools depth calculates how many times the given position or region is covered by the mapped read.
samtools depth reports three column output containing chromosome, base position, and read depth at each position.
If you want to calculate the average coverage depth of all the reads in a BAM file for all chromosomes, you need to use awk to calculate the average coverage depth based on the depth values in third column.
samtools depth input.bam | awk '{sum+=$3} END {print "Average coverage:", sum/NR}' coverage.txt
# output
Average = 1.21185
The average coverage depth for input.bam BAM file is 1.21 i.e. each base is sequenced at 1.21 times on average.
To get the coverage depth in terms of X, you need to divide this number (here, 1.21) by the haploid genome size (in bp).
samtools depthdoes not calculate the coverage depth for positions that are not mapped by the reads. In this case, you can add-aparameter to thesamtools depthto output all positions including zero depth .
Samtools coverage
samtools coverage command can be used for calculating the percent of coverage i.e. how many percent of bases are covered for each chromosome.
For example. if your chromosome size is 100 and only 10 bases are covered, then your coverage is 10%. Sometimes, this is also referred as
breadth of coverage.
samtools coverage command gives the output in table format for each chromosome.
Calculate the coverage for each chromosome from the BAM file,
samtools coverage input.bam
# output
#rname startpos endpos numreads covbases coverage meandepth meanbaseq meanmapq
chr1 1 249250621 444 13160 0.00527983 6.39838e-05 48.2 25
chr2 1 243199373 0 0 0 0 0 0
chr3 1 198022430 0 0 0 0 0 0
chr4 1 191154276 0 0 0 0 0 0
chr5 1 180915260 0 0 0 0 0 0
Based on the output above, the % coverage for chr1 is 0.0052%. This means that 13160 bases are covered for chr1 (out of 249250621).
Enhance your skills with courses on genomics and bioinformatics
- Genomic Data Science Specialization
- Biology Meets Programming: Bioinformatics for Beginners
- Python for Genomic Data Science
- Bioinformatics Specialization
- Command Line Tools for Genomic Data Science
- Introduction to Genomic Technologies
This work is licensed under a Creative Commons Attribution 4.0 International License
Some of the links on this page may be affiliate links, which means we may get an affiliate commission on a valid purchase. The retailer will pay the commission at no additional cost to you.
]]>