Calculate harmonic mean in R (with examples)
Harmonic mean
Harmonic mean (HM) is a reciprocal of the arithmetic mean of the reciprocal of given numbers.
There should be no zero number in the dataset, otherwise harmonic mean will be zero. The harmonic mean is commonly used for calculating the mean of rates or ratios (e.g. speed of the car) as it gives more accurate answers than arithmetic means.
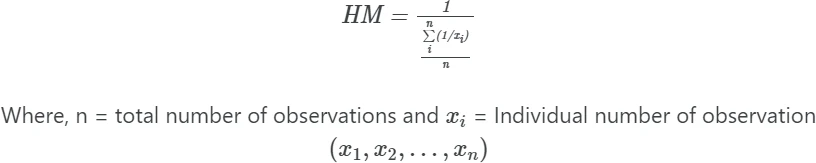
Steps in harmonic mean calculation
For example, if we have three numbers of observations (e.g., 2, 5, 8),
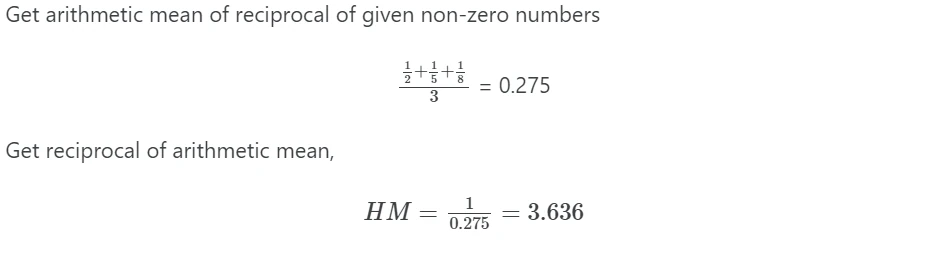
Calculate harmonic mean in R
Example: The speed of three motorbikes is 10 mph, 20 mph, and 60 mph. Calculate the harmonic mean of the motorbike’s speed.
You can calculate the harmonic mean of the speed of motorbike’s using the harmonic.mean()
function available in the psych package. harmonic.mean() function takes the following arguments,
x: a vector, matrix, or data.frame
na.rm: if TRUE, drop NA values
zero: if TRUE, return 0 if there are any 0 values. Otherwise, return harmonic mean of non-zero numbers
library("psych")
x <- c(10, 20, 60)
harmonic.mean(x)
# output
18
The harmonic mean of the speed of three motorbikes is 18 mph.
If you have a data frame, you can also calculate the harmonic mean from data frame columns,
# create a sample data frame
df <- data.frame(bike=c("A", "B", "C"),
speed=c(10, 20, 60))
# view data frame
df
bike speed
1 A 10
2 B 20
3 C 60
# calculate harmonic mean
library("psych")
harmonic.mean(df$speed)
# output
18
Calculate harmonic mean from scratch in R
First, calculate the arithmetic mean of the reciprocal of given non-zero numbers,
m <- mean(c(1/10, 1/20, 1/60))
Now, get the reciprocal of the arithmetic mean,
hm <- 1/m
hm
# output
18
The harmonic mean of the speed of three motorbikes is 18 mph.
Enhance your skills with courses on Statistics and R
- Introduction to Statistics
- R Programming
- Data Science: Foundations using R Specialization
- Data Analysis with R Specialization
- Getting Started with Rstudio
- Applied Data Science with R Specialization
- Statistical Analysis with R for Public Health Specialization
This work is licensed under a Creative Commons Attribution 4.0 International License

