Calculate harmonic mean in Python (with examples)

Renesh Bedre    1 minute read

Harmonic mean (HM) is defined as a reciprocal of the arithmetic mean of the reciprocal of given numbers.

There should be no zero number in the dataset, otherwise harmonic mean will be zero. The harmonic mean is commonly used for calculating the mean of rates or ratios (e.g. speed of the car) as it gives more accurate answers than arithmetic means.

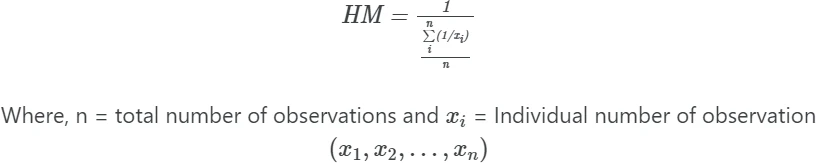
harmonic mean formula

Calculate harmonic mean in Python

Example: The speed of three cars are 20 mph, 40 mph, and 80 mph. Calculate the harmonic mean of the cars speed.

You can calculate the harmonic mean of the speed of cars using the hmean() function available in the scipy package. hmean() function takes the following arguments,

a: input array of numbers 

from scipy.stats import hmean

hmean(a = [20, 40, 80])
# output
34.2857

The harmonic mean of the speed of three cars is 34.2857 mph.

Calculate harmonic mean from scratch in Python

First, calculate the arithmetic mean of the reciprocal of given non-zero numbers,

import numpy as np
m = np.mean([1/20, 1/40, 1/80])

Now, get the reciprocal of the arithmetic mean,

hm = 1/m
hm
# output
34.2857

The harmonic mean of the speed of three cars is 34.2857 mph.

Enhance your skills with courses on Statistics and Python


This work is licensed under a Creative Commons Attribution 4.0 International License

You may also enjoy