Calculating residuals in regression analysis [Manually and with codes]

Renesh Bedre    5 minute read

Page content

What is residuals?

In regression analysis, we model the linear relationship between one or more independent (X) variables with that of the dependent variable (y).

The simple linear regression model is given as,

\( y = a + bX + \epsilon \)
Where, a = y-intercept, b = slope of the regression line (unbiased estimate) and \( \epsilon \) = error term (residuals)

This regression model has two parts viz. fitted regression line (a + bX) and error term (ε)

The error term (ε) in regression model is called as residuals, which is difference between the actual value of y and predicted value of y (regression line).

\( residuals = actual \ y (y_i) - predicted \ y \ (\hat{y}_i) \)

Regression plot

How to calculate residuals?

The residual is calculated by subtracting the actual value of the data point from the predicted value of that data point. The predicted value can be obtained from regression analysis.

For example, let’s take an example of the height and weight of students (source)

Height (X) Weight (y)
1.36 52
1.47 50
1.54 67
1.56 62
1.59 69
1.63 74
1.66 59
1.67 87
1.69 77
1.74 73
1.81 67

If we perform simple linear regression on this dataset, we get fitted line with the following regression equation,

ŷ = -22.4 + (55.48 * X)

Learn more here how to perform the simple linear regression in Python

With the regression equation, we can predict the weight of any student based on their height.

For example, if the height of student is 1.36, its predicted weight is 53.08

ŷ = -22.37 + (55.48 * 1.36) = 53.08

Similarly, we can calculate the predicted weight (ŷ) of all students,

Height (X) Weight (y) Predicted weight (ŷ)
1.36 52 53.08
1.47 50 59.18
1.54 67 63.07
1.56 62 64.18
1.59 69 65.84
1.63 74 68.06
1.66 59 69.72
1.67 87 70.28
1.69 77 71.39
1.74 73 74.16
1.81 67 78.04

Now, we have actual weight (y) and predicted weight (ŷ) for calculating the residuals,

Calculate residual when height is 1.36 and weight is 52,

\( residuals = actual \ y (y_i) - predicted \ y \ (\hat{y}_i) = 52-53.08 = -1.07 \)

Similarly, we can calculate the residuals of all students,

Height (X) Weight (y) Predicted weight (y_pred) Residual
1.36 52 53.08 -1.07
1.47 50 59.18 -9.18
1.54 67 63.07 3.93
1.56 62 64.18 -2.18
1.59 69 65.84 3.15
1.63 74 68.06 5.93
1.66 59 69.72 -10.71
1.67 87 70.28 16.72
1.69 77 71.39 5.61
1.74 73 74.16 -1.15
1.81 67 78.05 -11.04

The sum and mean of residuals is always equal to zero

If you plot the predicted data and residual, you should get residual plot as below,

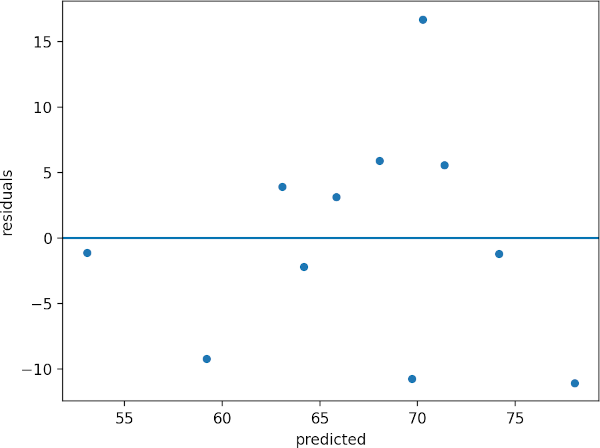
Residual plot in python

The residual plot helps to determine the relationship between X and y variables. If residuals are randomly distributed (no pattern) around the zero line, it indicates that there linear relationship between the X and y (assumption of linearity). If there is a curved pattern, it means that there is no linear relationship and data is not appropriate for regression analysis.

In addition, residuals are used to assess the assumptions of normality and homogeneity of variance (homoscedasticity).

Calculate residuals in Python

Here are the steps involved in calculating residuals in regression analysis using Python,

For following steps, you need to install pandas, statsmodels, matplotlib, and seaborn Python packages. Check how to install Python packages

Get the dataset

import pandas as pd

df = pd.read_csv("https://reneshbedre.github.io/assets/posts/reg/height.csv")
# view first two rows
df.head(2)
   Height  Weight
0    1.36      52
1    1.47      50

Fit the regression model

We will fit the simple linear regression model as there is only one independent variable

import statsmodels.api as sm

X = df['Height']  # independent variable
y = df['Weight']   # dependent variable

# to get intercept -- this is optional
X = sm.add_constant(X)

# fit the regression model
reg = sm.OLS(y, X).fit()

# to get output summary, use reg.summary()

Get the residuals

reg.resid
# output
0     -1.079016
1     -9.182056
2      3.934191
3     -2.175453
4      3.160082
5      5.940795
6    -10.723671
7     16.721507
8      5.611864
9     -1.162245
10   -11.045998
dtype: float64

Create residuals plot

Create scatterplot of predicted values and residuals,

from bioinfokit import visuz
import seaborn as sns
import matplotlib.pyplot as plt

# create a DataFrame of predicted values and residuals
df["predicted"] = reg.predict(X)
df["residuals"] = reg.resid
sns.scatterplot(data=df, x="predicted", y="residuals")
plt.axhline(y=0)

Residual plot in python

Calculate residuals in R

Here are the steps involved in calculating residuals in regression analysis using R,

Get the dataset

library(tidyverse)
df <- read.csv("https://reneshbedre.github.io/assets/posts/reg/height.csv")
# view first two rows
head(df, 2)
  Height Weight
1   1.36     52
2   1.47     50

Fit the regression model

reg <- lm(Weight ~ Height, data = df) 
# to get output summary, use summary(reg)

Get the residuals

resid(reg)
         1          2          3          4          5          6          7 
 -1.079016  -9.182056   3.934191  -2.175453   3.160082   5.940795 -10.723671 
         8          9         10         11 
 16.721507   5.611864  -1.162245 -11.045998

Create residuals plot

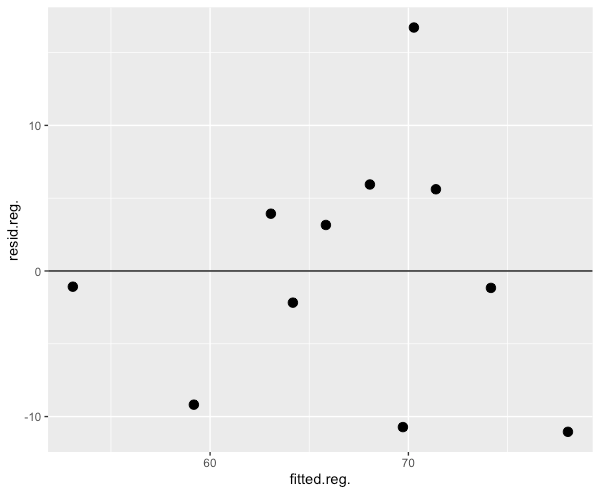
Create scatterplot of predicted values and residuals in R,

# create a data frame
df1 <- data.frame(fitted(reg), resid(reg))
ggplot(df1, aes(fitted.reg., resid.reg.)) + geom_point(size = 3) + geom_hline(yintercept = 0)

Residual plot in R

Enhance your skills with courses on regression

References

  1. Kim HY. Statistical notes for clinical researchers: simple linear regression 3–residual analysis. Restorative dentistry & endodontics. 2019 Feb 1;44(1).

If you have any questions, comments or recommendations, please email me at reneshbe@gmail.com


This work is licensed under a Creative Commons Attribution 4.0 International License

Some of the links on this page may be affiliate links, which means we may get an affiliate commission on a valid purchase. The retailer will pay the commission at no additional cost to you.

You may also enjoy