How to Perform Mann-Whitney U test in Python

Mann-Whitney U test

• Mann-Whitney U test is a non-parametric test which is alternative to the parametric two sample t-test. It is first proposed by Frank Wilcoxon (1945) and later worked by Henry Mann and Donald Whitney (1947). Hence, the Mann-Whitney U test is also known as Wilcoxon rank sum test or Wilcoxon‐Mann‐Whitney (WMW) test.

  Wilcoxon rank sum test is different than Wilcoxon signed rank sum test. On paired data, the Wilcoxon signed rank sum test is used.

• Mann-Whitney U test used for comparing differences between two independent groups. It tests the hypothesis that if the two groups come from same population or have the same medians. It does not assume any specific distribution (such as normal distribution of samples) for calculating test statistics and p values. If there are more than two groups to analyze, you should consider Kruskal-Wallis test.
• The sample mean ranks or medians (not means) are compared in the Mann-Whitney U test based on the shape of distribution of two independent groups, which distinguishes it from the t-test, which compares sample means.
• Mann-Whitney U test can be applied on small (5-20) and large samples (n > 20). The power increases with sample size.
• Though Mann-Whitney U test and t-test has similar statistical power, it is always wise to use t-test if its assumptions are met.

Mann-Whitney U test assumptions

• The observations from the two groups should be randomly selected from the target populations
• Observations are independent of each other
• Observations should be continuous or ordinal (e.g. Likert item data)

Mann-Whitney U test Hypotheses

If we have two independent groups with observations x₁, x₂, …, x_m and y₁, y₂, …, y_n sampled from X and Y populations, then Mann-Whitney U test compares each observation x_i from sample x with each observation (y_j) from sample y.

Null hypothesis: p (x_i > y_j ) = 0.5
Alternative hypothesis: p (x_i > y_j ) ≠ 0.5

Above two-sided alternative hypothesis tests that there is equal probability of x_i is greater or lesser than y_j (both groups came from same population),

One-sided alternative hypothesis tests probability of x_i is greater than y_j and vice versa.

We can also state the two-sided hypothesis in terms of median as (when two groups have same shape of distribution)

Null hypothesis: Two groups have equal median

Alternative hypothesis: Two groups does not have equal median

One-sided alternative hypothesis tests median from one group can be greater or lesser than other group.

Learn more about hypothesis testing and interpretation

Mann-Whitney U Test formula

The p value is calculated based on the comparison between the critical value and the U value. If U value <= critical value, we reject the null hypothesis and vice versa. If the sample is large (n>20), the p value is calculated based on the normal approximation using standardized test statistics.

How Mann-Whitney U Test works?

• Merge the data from two samples and rank them from smallest to largest
• Calculate the sum of rank for each sample (Rx and Ry)
• Calculate Mann-Whitney test statistic (U) using the formula (minimum of Ux and Uy)
• Calculate p value by comparing U with the critical value

Perform Mann-Whitney U test in Python

Mann-Whitney U test example

Suppose, there are two plant genotypes (A and B) differing in their yield phenotype. Mann-Whitney U test is appropriate to compare the yield of two genotypes under the assumption that yield output does not follow the normal distribution.

Get example dataset and summary statistics

Load hypothetical plant genotypes (A and B) yield dataset,

Learn how to import data using pandas

import pandas as pd
df = pd.read_csv("https://reneshbedre.github.io/assets/posts/mann_whitney/genotype.csv")
df.head(2)
    A   B
0  60  10
1  30  25

# get summary statistics
df.agg(["count", "min", "max", "median", "mean", "skew"])
                A          B
count   23.000000  23.000000
min     20.000000  10.000000
max     60.000000  32.000000
median  56.000000  28.000000
mean    47.695652  25.217391
skew    -0.710884  -1.270302

# generate boxplot to check data spread
import matplotlib.pyplot as plt
df.boxplot(column=['A', 'B'], grid=False)
plt.show()

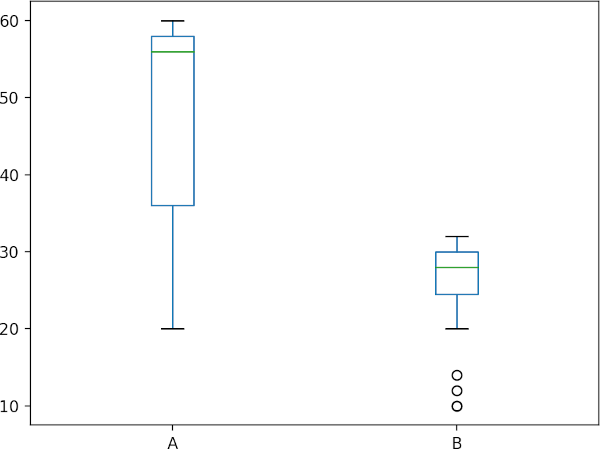
Check data distribution

Check data distribution using Shapiro-Wilk test and histogram ,

import scipy.stats as stats
w, pvalue = stats.shapiro(df['A'])
w, pvalue
(0.8239281177520752, 0.0009495539125055075)

w, pvalue = stats.shapiro(df['B'])
w, pvalue
(0.7946348190307617, 0.00031481595942750573)

# plot histogram
import matplotlib.pyplot as plt
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.suptitle('Frequency histogram of genotypes yield')
ax1.hist(df['A'], bins=10, histtype='bar', ec='k') 
ax2.hist(df['B'], bins=10, histtype='bar', ec='k') 
ax1.set_xlabel("Yield")
ax2.set_xlabel("Yield")
plt.show()

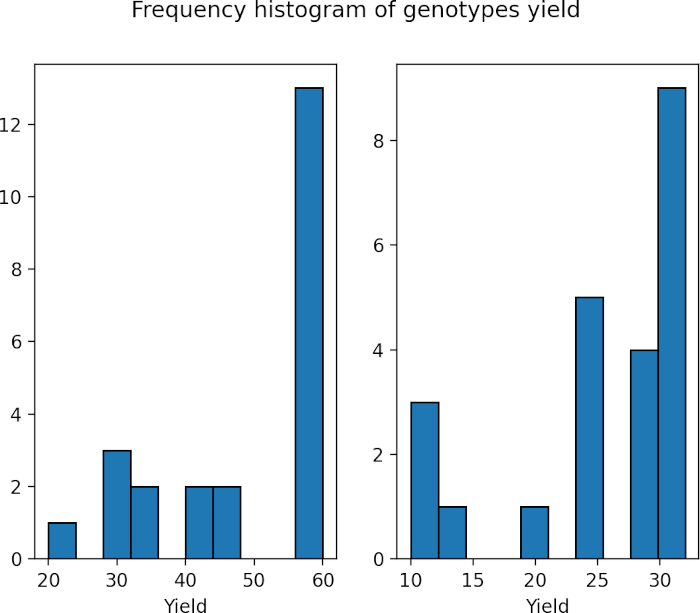
As the p value obtained from the Shapiro-Wilk test is significant (p < 0.05), we conclude that the data is not normally distributed. Further, in histogram data distribution shape does not look normal. Therefore, Mann-Whitney U test is more appropriate for analyzing two samples.

Perform Mann-Whitney U test

Perform two-sided (yield of two genotypes does not have equal medians) Mann-Whitney U test,

Note: We are comparing median as two genotypes have similar shape of distribution (see histogram and boxplot). If two groups do not have similar shape of distribution, you should compare mean ranks.

# SciPy v1.7.1
import scipy.stats as stats
# perform two-sided test. You can use 'greater' or 'less' for one-sided test
stats.mannwhitneyu(x=df['A'], y=df['B'], alternative = 'two-sided')
# output
MannwhitneyuResult(statistic=489.5, pvalue=7.004695394561267e-07)

Check online calculator for performing Mann-Whitney U test

Note: In the above example, the p value obtained from mannwhitneyu is based on the normal approximation as the sample size is large (n > 20). If the sample size is small, a normal approximation is not appropriate. To get exact p value, set method=”exact”. The mannwhitneyu function automatically calculates the exact p value when one of the sample size is < 8. Both exact and normal approximation p values should be roughly similar.

Mann-Whitney U test interpretation: As the p value obtained from the Mann-Whitney U test is significant (U = 489.5, p < 0.05), we conclude that the yield of the two genotypes significantly different from each other .

Perform one-sided (median yield of A genotype is greater than median yield of genotype B) Mann-Whitney U test,

import scipy.stats as stats
stats.mannwhitneyu(x=df['A'], y=df['B'], alternative = 'greater')
# output
MannwhitneyuResult(statistic=489.5, pvalue=3.5023476972806333e-07)

As the p value obtained from the Mann-Whitney U test is significant (U = 489.5, p < 0.05), we conclude that the yield of the A genotype significantly greater than the genotype B.

Learn how to perform Mann-Whitney U test in R

Related reading

• Friedman test using R (with examples and code)
• What is p value and how to calculate p value by hand

References

1. Nachar N. The Mann-Whitney U: A test for assessing whether two independent samples come from the same distribution. Tutorials in quantitative Methods for Psychology. 2008 Mar;4(1):13-20.
2. Mann–Whitney Test
3. Mann Whitney U Test (Wilcoxon Rank Sum Test)

If you have any questions, comments or recommendations, please email me at reneshbe@gmail.com

This work is licensed under a Creative Commons Attribution 4.0 International License