Mastering Z-test in Python: A Step-by-Step Guide (With Examples)
1. Background
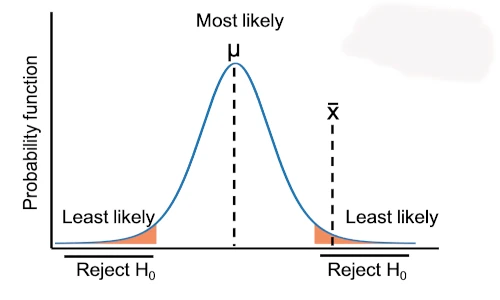
- Z-test is a parametric statistical method for comparing the means of the two populations (two-sample independent and paired Z-test) and for comparing the mean of a sample to a specific value (one sample Z-test).
- Z-test requires a large sample size (n ≥ 30) and known population variance (or deviation). If the population variance is not known, use a t-test, which uses sample standard deviation (s).
- In Z-test, the test statistic follows the standard normal distribution (Z-distribution) (type of continuous probability distribution) under the null hypothesis.
- Z-test has three main types: One Sample Z-test, two sample Z-test (unpaired or independent), and paired Z-test.
If you have proportion data, the check for Z-Test for proportion
2. Types of Z-test
2.1 One Sample Z-test
- One Sample Z-test (single sample Z-test) is used to compare the sample mean with some specific or hypothesized value (known mean of the population). One Sample Z-test checks whether the sample comes from a known population where population mean and standard deviation (σ) should be known.
If the sample size is large (n ≥ 30) and population standard deviation is unknown, you can also estimate the population standard deviation from the sample.
2.1.1 Assumptions
- The dependent variable should have an approximately standard normal distribution i.e. N(0, 1) (Shapiro-Wilks Test)
- Population standard deviation should be known
- The dependent variable should be a continuous variable
- Observations are independent of each other and randomly drawn from a population
- The sample size should be large (n ≥ 30)
2.1.2 Hypotheses
- Null hypothesis: Sample mean is equal to the hypothesized or known population mean
- Alternative hypothesis: Sample mean is not equal to the hypothesized or known population mean (two-tailed)
- Alternative hypothesis: Sample mean is either greater or lesser than the hypothesized or known population mean (one-tailed)
| Null hypothesis (H0) | Alternative hypothesis (Ha) | type | Reject H0 when (at 5% significance level) |
|---|---|---|---|
| µ = µ0 | µ ≠ µ0 | two-tailed | |Z| > 1.96 |
| µ ≥ µ0 | µ < µ0 | one-tailed (lesser) | Z < -1.64 |
| µ ≤ µ0 | µ > µ0 | one-tailed (greater) | Z > 1.64 |
Learn more about hypothesis testing and interpretation
2.1.3 Formula
One sample Z-test formula,

If |Z | > critical value (1.96 for two-tailed test and 1.64 for one-tailed test), reject the null hypothesis i.e. p value is statistically significant (p < 0.05).
2.1.4 Calculate one sample Z-test in Python
Example: A factory produces balls of a diameter of 5 cm. But due to manufacturing conditions, every ball may not have the exactly same diameter. The standard deviation of the diameters of balls is 0.4. Now, the quality officer would like to test whether the ball diameter is significantly different from 5 cm in a sample of 50 balls randomly taken from the manufacturing line.
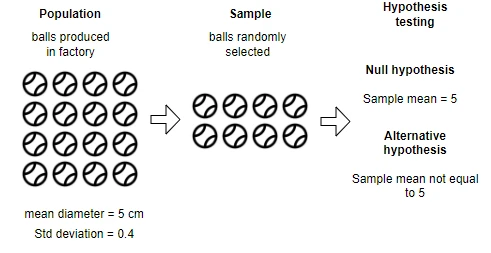
Import dataset for testing ball diameter using Z-test,
Note: If you have your own dataset, you should import it as pandas DataFrame. Learn how to import data using pandas
from bioinfokit.analys import get_data
df = get_data('z_one_samp').data
df.head(2)
# output
sizes
0 4.819289
1 3.569358
df.shape
# output
(50, 1)
Now, perform one sample Z-test using the ztest()
function available in the bioinfokit package. ztest() function takes the following arguments,
df: pandas DataFrame containing x group
x: column name for x group
mu: hypothesized or known population mean (specified in null hypothesis)
x_std: Population standard deviation for x group
alpha: Significance level for confidence interval (default:0.05)
test_type: Type of Z-test. Use 1 for One sample Z-test
from bioinfokit.analys import stat
res = stat()
res.ztest(df=df, x='sizes', mu=5, x_std=0.4, test_type=1)
print(res.summary)
# output
One Sample Z-test
------------------ ---------
Sample size 50
Mean 5.01796
Z value 0.317465
p value (one-tail) 0.375446
p value (two-tail) 0.750891
Lower 95.0% 4.90709
Upper 95.0% 5.12883
------------------ ---------
# access Z value and p value (two-tailed)
z, p = res.result[1], res.result[3]
z, p
# output
(0.317464581858033, 0.7508911101410283)
2.1.5 Interpretation
The p value obtained from the one sample Z-test is not significant [Z value = 0.3174, p = 0.7508), and therefore, we conclude that the mean diameter of the balls in a random sample is equal to the population mean of 5 cm. In other words, the sample is drawn from the same population.
2.2 Two sample Z-test (unpaired or independent Z-test)
The two-sample (unpaired or independent) Z-test calculates if the means of two independent groups are equal or significantly different from each other. Unlike the t-test, Z-test is performed when the population means and standard deviation are known.
If the sample size is large (n ≥ 30) and population standard deviation is unknown, you can also estimate the population standard deviation from the sample.
2.2.1 Hypotheses
- Null hypothesis: Two group means are equal
- Alternative hypothesis: Two group means are different (two-tailed)
- Alternative hypothesis: Mean of one group either greater or lesser than another group (one-tailed)
| Null hypothesis (H0) | Alternative hypothesis (Ha) | type | Reject H0 when (at 5% significance level) |
|---|---|---|---|
| µ1 = µ2 | µ1 ≠ µ2 | two-tailed | |Z| > 1.96 |
| µ1 ≥ µ2 | µ1 < µ2 | one-tailed (lesser) | Z < -1.64 |
| µ1 ≤ µ2 | µ1 > µ2 | one-tailed (greater) | Z > 1.64 |
Learn more about hypothesis testing and interpretation
2.2.2 Assumptions
- Dependent variable for sample should have an approximately standard normal distribution (Shapiro-Wilks Test)
- Population standard deviations (σ1 and σ2) should be known
- Dependent variable should be continuous variable
- Observations are independent of each other and randomly drawn from a population
- The sample size should be large (n ≥ 30)
If the sample size small and does not follow the normal distribution, you should use non-parametric Mann-Whitney U test (Wilcoxon rank sum test)
2.2.3 Formula
Two sample (independent) Z-test formula,

2.2.4 Calculate Two sample Z-test in Python
Example: a factory in A and B cities produces balls of a diameter of 5 cm. The defect is reported in the B factory which is known to cause a change in ball size. The standard deviation of the diameters of the balls is 0.1. The factory quality officer randomly selects 50 balls from both factories to test whether the ball diameter is significantly different in factory B than that produced in factory A.
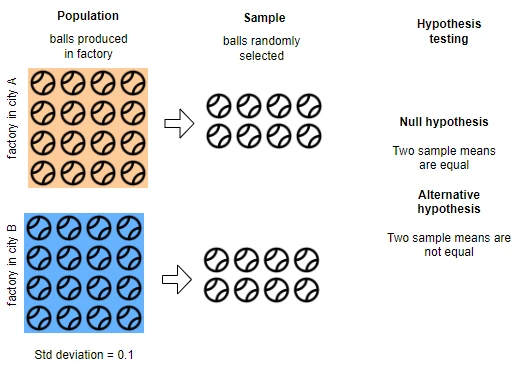
Import dataset for testing ball diameter using two sample Z-test,
Note: If you have your own dataset, you should import it as pandas dataframe. Learn how to import data using pandas
from bioinfokit.analys import get_data
df = get_data('z_two_samp').data
df.head(2)
# output
fact_A fact_B
0 4.977904 5.887947
1 5.166254 5.990616
df.shape
# output
(50, 2)
Now, perform two sample Z-test using the ztest()
function available in the bioinfokit package. ztest() function takes the following arguments,
df: pandas DataFrame containing x group
x: column name for x group
y: column name for y group
x_std: Population standard deviation for x group
y_std: Population standard deviation for y group
alpha: Significance level for confidence interval (default:0.05)
test_type: Type of Z-test. Use 2 for two sample Z-test
from bioinfokit.analys import stat
res = stat()
res.ztest(df=df, x='fact_A', y='fact_B', x_std=0.1, y_std=0.1, test_type=2)
print(res.summary)
# output
Two Sample Z-test
------------------ ----------
Sample size for x 50
Sample size for y 50
Mean of x 5.01284
Mean of y 5.99015
Z value -48.8656
p value (one-tail) 0
p value (two-tail) 0
Lower 95.0% -1.01651
Upper 95.0% -0.938113
------------------ ----------
# access Z value and p value (two-tailed)
z, p = res.result[2], res.result[4]
z, p
# output
(-48.865610925707244, 0.0)
2.2.5 Interpretation
The p value obtained from the two samples Z-test is highly significant [Z = -48.8656, p < 0.001]. This indicates that there is a significant difference in the ball size produced in factories A and B. We conclude that there is a defect in the machine for ball production in factory B.
2.3 Paired Z-test (dependent Z-test)
- Paired Z-test is used for checking whether there is difference between the two paired samples or not. For example, we have plant variety A and would like to compare the yield of variety A before and after the application of fertilizer.
2.3.1 Hypotheses
- Null hypothesis: There is no difference between the two sample means (difference=0)
- Alternative hypothesis: There is a difference between the two sample means (two-tailed)
- Alternative hypothesis: Difference between two sample means either greater or lesser than zero (one-tailed)
| Null hypothesis (H0) | Alternative hypothesis (Ha) | type | Reject H0 when (at 5% significance level) |
|---|---|---|---|
| δ = 0 | δ ≠ 0 | two-tailed | |Z| > 1.96 |
| δ ≤0 | δ > 0 | one-tailed (greater) | Z > 1.64 |
| δ ≥ 0 | δ < 0 | one-tailed (lesser) | Z < -1.64 |
2.3.2 Assumptions
- Differences between the two dependent variables follow an approximately standard normal distribution (Shapiro-Wilks Test)
- The independent variable should have a pair of dependent variables
- Observations are sampled independently from each other
- Dependent variables should be a continuous variable
- Population standard deviations (σδ) for difference should be known
- The sample size should be large (n ≥ 30). If you have a small sample size, you can use the t test
2.3.3 Formula
Paired Z-test formula,

2.3.4 Calculate paired Z-test in Python
Example: a researcher wants to test the effect of fertilizer on plant growth. The researcher measures the height of the plants before and after the application of fertilizer. The standard deviations for two plant height differences (before and after the application of fertilizer) is 1.2. A researcher wants to test if there is an increase in plant heights after the application of fertilizers.
Import dataset for paired Z-test,
Note: If you have your own dataset, you should import it as pandas dataframe. Learn how to import data using pandas
import pandas as pd
# load dataset as pandas dataframe
df = pd.read_csv('https://reneshbedre.github.io/assets/posts/ztest/paired_z.csv')
df.head(2)
# output
before after
0 75.731539 83.154634
1 75.273005 83.322584
df.shape
# output
(60, 2)
If the assumed population difference is zero (as stated in the null hypothesis), the paired Z-test reduces to the one sample Z-test. Hence, we will perform one sample Z-test on paired differences.
from bioinfokit.analys import stat
# get difference
df['diff'] = df['after'] - df['before']
df.head(2)
# output
before after diff
0 75.731539 83.154634 7.423096
1 75.273005 83.322584 8.049578
# perform Z-test on paired differences
res = stat()
res.ztest(df=df, x='diff', mu=0, x_std=1.2, test_type=1)
print(res.summary)
# output
One Sample Z-test
------------------ -------
Sample size 60
Mean 10.4227
Z value 67.278
p value (one-tail) 0
p value (two-tail) 0
Lower 95.0% 10.119
Upper 95.0% 10.7263
------------------ -------
# access Z value and p value (two-tailed)
z, p = res.result[1], res.result[3]
z, p
# output
(67.27803205046483, 0.0)
2.3.5 Interpretation
The p value obtained from the paired Z-test is highly significant [Z = 67.278, p < 0.001 (one-tailed)]. This indicates that there is a significant increase in the plant height after the application of fertilizer. We conclude that fertilizer has a significant contribution to increasing plant height.
Enhance your skills with courses on statistics
- Statistics with Python Specialization
- Advanced Statistics for Data Science Specialization
- Introduction to Statistics
- Python for Everybody Specialization
- Understanding Clinical Research: Behind the Statistics
References
- Heumann C, Shalabh MS. Introduction to statistics and data analysis. Springer; 2016.
If you have any questions, comments, corrections, or recommendations, please email me at reneshbe@gmail.com
This work is licensed under a Creative Commons Attribution 4.0 International License
Some of the links on this page may be affiliate links, which means we may get an affiliate commission on a valid purchase. The retailer will pay the commission at no additional cost to you.

